

The "base SA" refers to the circle that comprises the base in a closed circular cone, while the lateral SA refers to the rest of the area of the cone between the base and its apex. The surface area of a circular cone can be calculated by summing the surface area of each of its individual components. Given that each truffle has a radius of 0.325 inches: When she receives a box of Lindt truffles, she proceeds to calculate the surface area of each truffle in order to determine the total surface area she has to lick to decrease the probability that anyone will try to eat her truffles. Xael doesn't like sharing her chocolate truffles with anyone. The surface area (SA) of a sphere can be calculated using the equation: Please refer to the aforementioned calculators for more detail on each individual object. As such, this calculator will focus on the equations for calculating the surface area of the objects and the use of these equations. All of the objects addressed in this calculator are described in more detail on the Volume Calculator and Area Calculator pages. The surface area of a solid is a measure of the total area occupied by the surface of an object. Related Volume Calculator | Area Calculator | Body Surface Area Calculator Square Pyramid Surface Area Base Edge (a) Base Radius (r)Ĭonical Frustum Surface Area Top Radius (r) Please provide any two values below to calculate. Ball Surface Area Radius (r)Ĭylindrical Tank Surface Area Base Radius (r) Use the calculators below to calculate the surface area of several common shapes. The surface area of the prism is 2 0 4 u n i t .Home / math / surface area calculator Surface Area Calculator Where 𝑎 and 𝑏 are its two parallel sides and ℎ its height. Let us work out the area of the base of the prism. We can of course work out the area of each rectangular face individually and sum up all together we find the same result. Its area is given by multiplying its length by its width. We clearly see on the net that they form a large rectangle of length the perimeter of the base and width the height of the prism, The lateral surface area of the prism is the area of all its rectangular faces that join the two bases. Rectangle whose dimensions are the height of the prism and the perimeter of the prism’s base. The surface area of a prism: on the net of a prism, all its lateral faces form a large In the previous example, we have found an important result that can be used when we work out The surface area of the prism is 7 6 u n i t .
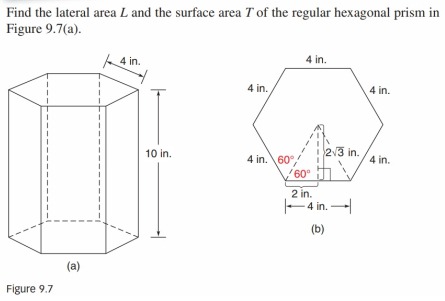
t o t a l b a s e l a t e r a l u n i t To find the total surface area of the prism, we simply need to add two times the area of theīase (because there are two bases) to the lateral area. We do find the same area however we compose rectangles to make the base. We can of course check that we find the same area with adding the area of two rectangles Or as the rectangle of length 5 and width 4 from which the rectangle of length The base can be seen as made of two rectangles, We need to find the area of the two bases. Prism, which is given by multiplying its length by its width: Now, we can work out the area of the large rectangle formed by all the lateral faces of the The missing lengths can be easily found given that all angles in the bases are right angles. The width of the rectangle formed by all lateral faces is actually the perimeter of the base. Where 𝑎 and 𝑏 are the two missing sides of the base of the prism. They form a large rectangle of length 3 and width We see that all the rectangles have the same length: it is the height of the prism, On the net, the rectangular faces between the two bases are clearly to be seen.


 0 kommentar(er)
0 kommentar(er)
